Suppose you have invested in a stock which does not pay any dividends but you anticipate it to grow at a given rate. Now someone comes and tells you that a better alternative is a dividend growth stock whose dividend grows at a known rate and it will provide you the benefit of double compounding. How do you compare the two alternatives?
One way to do it is to compute the effective growth rate of the dividend growth stock over the time horizon of your investment. If the effective growth rate of the dividend growth stock is higher than the growth rate you anticipate for the non-dividend paying stock that you have, you should rush to accept the advice of your friend and buy the dividend stock.
Think of the effective growth rate as follows: you buy the stock, and set up your account such that all the dividends are used to buy the stock whenever the dividends are paid (assumed to be paid annually here). Now use the value of your holding at the end of the time horizon and the initial value to compute the growth rate assuming that you had put the money in a CD which compounds annually at a fixed rate. The growth rate thus computed is the effective growth rate, and it is what should be compared with the growth rate of the non-dividend paying stock.
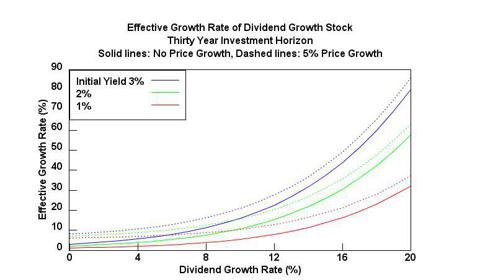
The effective growth rate of a dividend growth stock depends on four parameters: (i) the growth rate of the price of the stock itself, (ii) the initial yield, (iii) growth rate of the dividend, and (iv) the time horizon of the investment.
The following plot assumes the time horizon to be thirty years, and shows the effective growth rate of a dividend growth stock as a function of the dividend growth rate. The solid lines are for the cases when there is no price appreciation, and the dashed lines for the case of 5% price appreciation.